「P4550」收集邮票

08 / 28 / 2020 | 最后修改于 08 / 28 / 2020

OI Solution

一眼看上去就是期望 DP，然而蒟蒻不会，在同机房神仙讲解下豁然开朗，于是写篇题解。

Solution

直接设期望买完的钱数不很好搞，因为每次买邮票所需的钱数是随购买次数变化的，所以我们绕个路

设 $f_i$ 表示已经买到 $i$ 种邮票，若要买完剩下的邮票还需买多少次，转移如下：

f_i = \frac i n f_i + \frac {n-i} n f_{i+1} + 1

初始状态是 $f_n = 0$ ， $\frac i n f_i$ 含义是你有 $\frac i n$ 的概率买到已经买到的 $i$ 种邮票之一，状态仍然是 $f_i$ ， $\frac {n-i} n f_{i+1}$ 含义是你有 $\frac {n-i} n$ 的概率买到还没买到的 $n - i$ 种邮票之一，状态是 $f_{i+1}$ ，最后在加上这次买的一次贡献。

再设 $g_i$ 表示已经买到 $i$ 种邮票，若要买完剩下的邮票还需买多少钱，转移如下：

g_i = \frac i n (g_i + f_i + 1) + \frac {n-i} n (g_{i+1} + f_{i+1} + 1)

初始状态是 $g_n = 0$ ，仍然很好想。那 $\frac i n (g_i + f_i + 1)$ 是什么意思呢？放图镇楼：

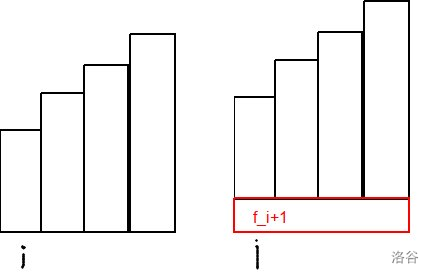
里面加的那个 $f_i + 1$ 其实就是给后面的每一次购买都+1，因为当你这次购买后，比如后面的某次是原来是第 $h$ 次，现在就是第 $h + 1$ 次，价格+1，那么后面有几次购买呢？就是 $f_i$ 次，最后别忘了你这第 $i$ 次也要+1。 $\frac {n-i} n (g_{i+1} + f_{i+1} + 1)$ 同理。

最后，把 $f_i, g_i$ 移项化简一下就好了：

f_i = f_{i+1} + \frac n {n-i} \\ g_i = \frac i {n-i} f_i + g_{i+1} + f_{i+1} + \frac n {n-i}

Talk is cheap, show me your code:

#include <cstdio>

const int N = 10005;
int n;
double f[N], g[N];

int main() {
#ifndef ONLINE_JUDGE
#ifdef LOCAL
  freopen("testdata.in", "r", stdin);
  freopen("testdata.out", "w", stdout);
#endif
#ifndef LOCAL
  freopen("CppTest.in", "r", stdin);
  freopen("CppTest.out", "w", stdout);
#endif
#endif

  scanf("%d", &n);
  for (int i = n - 1; ~i; --i) {
    f[i] = f[i + 1] + 1.0 * n / (n - i);
  }
  for (int i = n - 1; ~i; --i) {
    g[i] = 1.0 * i / (n - i) * f[i] + g[i + 1] + f[i + 1] + 1.0 * n / (n - i);
  }
  printf("%.2lf", g[0]);
  return 0;
}

「P4550」 收集邮票

08 / 28 / 2020 | 最后修改于 08 / 28 / 2020

Solution

「P4550」收集邮票